Appendix 4
How Dr Michael Huss, FRINA, and Karppinen made incorrect Water Inflow Calculations
This appendix shows how dr Michael Huss, expert to the 'Estonia' accident investigation Commission, falsified the water inflow into the superstructure with an open bow ramp in a sea way and how dr. Tuomi Karppinen, member of the accident investigation Commission, falsified 'simulations' of the same matter.
According supplement no. 523 formula (8) written by dr Huss the instantaneous water inflow (ton/s) on the car deck into the superstructure of the 'Estonia' above waterline due to forward motion/speed at a time t is, Msp(t),(specific weight x speed x area)
Msp(t) = j · V · A(t) (ton/s)
where
j = specific weight of water (1,008 t/m3)
V = ship's speed (7,46 m/s)
A(t) = Int ((b(z)) dz) = area of ramp opening in the superstructure (m²) below the wave/waterline, where
b(z) = ramp breadth = 5,4 m, (constant when the ship is upright)
z = Zr(t) - C (m) vertical coordinate for height (m) of the opening (positive when the ramp is below water), where
Zr(t) = relative motion (m) at the ramp (see figures 12b and fig 14b in supplement 410) relative the wave/waterline and positive below the wave/waterline
C = the height of the ramp opening above the bow wave = 2,0 m.
This formula is in principle correct assuming the opening is clear. In reality it is blocked by trailers loaded inside the ramp.
Total water inflow (tons) during time 0 - t seconds on the car deck in the superstructure, when the ramp is below water, MA, is according formula (9) in supplement no. 523 of dr. Huss
MA = Int ((Msp(t) + f(t)) dt) (ton)
where
f(t) = inflow due to other factors like the velocity of the water itself in the wave, etc, (small influence) = 0 ton/s.
According Supplement no. 410 we know the relative motion Zr(t) in regular waves (figure 12b) and irregular sea (fig 14b) and we can thus calculate how much water flows into the superstructure during, e.g. one pitching down into a wave.
It is however a truth with modifications, as water on the car deck in the superstructure changes the trim of the ship, i.e. the relative motion increases and the inflow increases too.
To simplify the calculations constant (zero) trim and no heel during the inflow period and the extra weight are assumed by dr Huss. It is thus assumed by Huss that the extra weight of water inside the superstructure does not change the future relative motion, i.e. that the ship actually pitches up again.
It is then easy to calculate the inflow of water into the 'Estonia' superstructure in both regular and irregular waves during one minute or in below case, 39 second, - it is only a function of speed V.
Inflow in Regular Waves during 39 seconds
Zr(t) in Regular waves (figure 12b of supplement 410) (head waves 15 knots, H = 4,0 m, T = 9,3 sec) - 7 pitchings up/down between seconds 59 and 99 (period 5,71 seconds) - total time 40 seconds of which only about 15,4 seconds with the bow opening of the superstructure below water (38,5% of the time).
z (the height of water above the lower edge of the ramp moving into the superstructure) varies from 0 to 3,0 m about as follows during one 2,2 seconds dip into a wave
0.0 - 0,6 m for 2,2 seconds
0,6 - 1,2 m for 1,9 seconds
1,2 - 1,8 m for 1,4 seconds
1,8 - 2,4 m for 1,1 seconds
2,4 - 3,0 m for 0,8 seconds
|
The ramp opening 3,0 meter above the lower edge, 16,2 m², is average below water only during 1,48 seconds. The max height of the opening was >5 meters, thus only 60% of the opening was below water. Let's assume that all water flows below and beside the trailers loaded inside the ramp. Total inflow MA during one pitching up/down of which the opening of the superstructure is only 2,2 seconds below water is thus about 180 tons (i.e. the whole opening 3 x 5,4 m = 16,2 m² is below water average 1,48 seconds - speed 7,45 m/s, j = 1,008). During one minute there are 10, 5 pitchings. Due to speed forward the water collects aft in the superstructure and does not flow out. But as soon as the ship stops with the opening away from the waves, all water flows out again! |
|
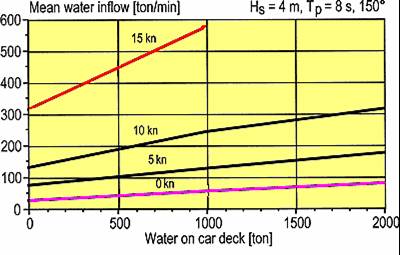
It means that total inflow in regular seas is 1 891 tons/minute with speed forward! According Huss (supplement 522 figure 4.2) the inflow is only 270 tons/minute. Hull falsifies the inflow by a factor of seven! In reality the inflow is probably much larger. The first 180 tons inside the superstructure trims the ship on the bow but has no time to flow out, the relative motion changes and the ship bow opening remains longer below water, more water flows in - the ship goes down like a submarine. It can easily be verified with model tests.
Inflow in irregular Waves
A similar calculation can be done for three pitching up/down in irregular seas (bow seas 14.5 knots, Hs=4,3 m) according figure 14b - one pitching zmax = 1,2 m for 2 seconds, another pitching zmax = 4,6 m for 2 seconds, a third pitching zmax = 3,4 m for 2 seconds, etc. These three pitching up/down take about 20 seconds. With similar calculations as above the writer finds that the inflow is 520 tons during 20 seconds, i.e 1 560 tons/min in irregular (bow) sea.
According Karppinen (supplement 523 figur 3 -x- ) the probability (sic) for this is <0,001. But evidently the inflows in regular and irregular sea are of the same order >1 500 tons/minute, and the probability (sic) for this inflow in irregular sea is one, i.e. it occurs all the time in any sequence of waves. The whole Karppinen report is pure falsification.
The above is calculated for speed V=15,0/14,5 knots. Naturally the inflow is reduced, if speed V is reduced. The relative motion amplitude hardly changes as long as the speed is >10 knots, but the number of pitching up/down per minute is reduced by reduced V, i.e. simply speaking the inflow is reduced by V2. At 10 knots the inflow into the superstructure is reduced by 49%, i.e. it is still considerable. And as the speed was >10 knots for more than two minutes after the ramp was allegedly pulled open, enough water to make the 'Estonia' capsize would have flowed in at that time.
Increased Inflow due to open Ramp
The above does not consider the open ramp. If the ramp is lowered (pulled fully open down to sea level), it acts as a plough and forces water up into the opening in the superstructure above the waves (there is at least 2x5,4=10,8 m2 ramp opening above the wave), and the opening becomes apparently bigger (say 67%); figure in 3.3. It means also that water flows in longer during each pitching down, as the ramp is under water longer than the opening in the superstructure itself (say 25%).
It means that the actual inflow will double.
Sound and Noise when Water is loaded on the Car Deck
To load >2 000 tons/min (or only 500 tons/min according Huss) water on a car deck in a superstructure on a ferry at sea should result ih big sound and noise and be noted by all aboard. The solid water is pushed in at high velocity and should destroy loose cargo in the way. Cars and trucks on the car deck must have been pushed aft and must have been demolished, electrical equipment must have been short circuited and damaged, passengers on deck 1 below the car deck should have heard an enormous thundering noise during several minutes when the water was pushed in ... but heard nothing. Huss and Karppinen never asked any survivors from deck 1 how they experienced water being loaded on top of them.
Conclusions
Huss has miscalculated the inflow of water into a superstructure for one minute with a factor of 7 - Huss states e.g. that the inflow in regular seas (head waves 15 knots H = 4,0 m, T = 9,3 sec) is only 270 tons/minute, when it should be at least 1 891 tons/minute, considerably more, if the ramp influence is considered. It is assumed that trailers and cars on the car deck are pushed aft by the water and do not influence the inflow.
Karppinen has also miscalculated the inflow in irregular seas (bow seas, 14,5 knots, Hs=4,3 m), where the total inflow is about 1 560 tons/minute for a typical sequence given in Supplement no. 410, while Karppinen states a very small probability (sic) (>0,001) for that value.
Neither Karppinen nor Huss considers the influence of the ramp - it doubles the inflows.
Neither Karppinen nor Huss considers that the first water/wave entering into the superstructure modifies the trim of the ship: when the opening in the superstructure comes below water (at 15 knots) the water (>150-180 tons) enters forward on the car deck and trims the ship (>1 meter!) on the bow and probably stops the relative motion, the ship will not pitch up again - you would expect the vessel to go immediately down like a submarine - the ship would never pitch up again! It can easily be confirmed by model tests.
But on the other hand, as soon as the vessel stops, all water flows out by itself.
Karppinen and Huss make so unrealistic calculations that you wonder, if the errors are intentional, as a part of the cover-up of the 'Estonia' investigation. Any university student can himself verify that the Huss/Karppinen calculations are manipulations.
Update 2007
In a report by SSPA Marine AB dated 27 March 2007 the tests indicated that initial flooding in the order of 2000-2500 tons/min could be expected with a fully open ramp.
---