Appendix 4
Hur Huss och Karppinen felberäknade vatteninflödet i överbyggnaden
Enligt supplement no. 523 formel (8) är vatteninflödet (ton per sekund) som följd av framfarten vid tiden t på bildäck i överbyggnaden, Msp(t),
Msp(t) = j V A(t) (ton/s), där
j = vattnets specifika vikt (1.008 t/m3)
V = fartygets hastighet (7.46 m/s)
A(t) = Int (b(z) dz) = rampöppningens yta (m²) under vattenytan i framfart i vågor där
b(z) = rampbredden = 5.4 m, (konstant när skeppet är upprätt)
z = Zr(t) - C (m) vertikal koordinat för höjden (m) i öppningen där
Zr(t) = relativa rörelsen (m) vid rampen (se fig 12b och fig 14b i supplement 410)
C = rampöppningens läge över bogvågen = 2.0 m.
Totala vatteninflödet (ton) på bildäck i överbyggnaden, MA, under tiden 0 - t sekunder är enligt formel (9)
MA = Int ((Msp(t) + f(t)) dt) (ton)
där
f(t) = inflöde beroende på andra faktorer (litet inflytande) = 0 ton/s.
Enligt Supplement no. 410 känner vi relativa rörelsen Zr(t) i regelbunden sjö (fig 12b) och oregelbunden sjö (fig 14b). Det är dock en sanning med modifikation, eftersom vatten på bildäck ändrar fartygets trim, dvs relativa rörelsen, och öppningen är längre tid under vatten, dvs inflödet ökar. För att förenkla beräkningen antages konstant trim och ingen krängning under hela inflödet och att lastbilar bakom rampen ej stoppar inflödet. Det är då lätt att beräkna vatteninflödet i regelbunden och oregelbunden sjö enbart som funktion av framfarten med hastighet V.
I princip behöver vi ju bara beräkna inflödet under en nerdoppning och sedan multiplicera med antalet nerdoppningar.
Zr(t) i Regelbunden sjö (fig 12b) (head waves 15 knop, H = 4.0, T = 9.3 sec) - 7 nerdoppningar mellan sekund 59 och 98 - 39 sekunder totalt varav 15.5 sekunder med öppningen i överbyggnaden under vatten.
z varierar från 0 till 3.0 m ungefär enligt nedan under en och varje nerdoppning:-
0.0 - 0.6 m under 2.2 sekunder
0.6 - 1.2 m under 1.9 sekunder
1.2 - 1.8 m under 1.4 sekunder
1.8 - 2.4 m under 1.1 sekunder
2.4 - 3.0 m under 0.8 sekunder
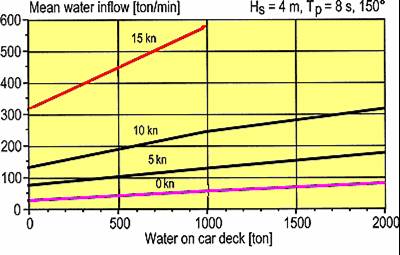
Totalt inflöde MA i överbyggnaden under en nerdoppning är alltså cirka 180 ton (dvs hela öppningen 3 x 5.4 m = 16.2 m² är under vatten under en medeltid av 1.48 sekunder - fart 7.45 m/s, j = 1.008). Och det är 10-11 nerdoppningar per minut. Inget vatten hinner rinna ut eftersom det är fart framåt - vattnet lastas hela tiden akterut i överbyggnaden. Det innebär att totala inflödet i regelbunden sjö är 1 940 ton/minut! Enligt Huss (supplement 522 figur 4.2) är inflödet bara 270 ton/min eller cirka 25 ton per nerdoppning. Huss har medvetet manipulerat sin rapport.
|
Det hela är helt logiskt - utan sjögång är överbyggnaden alltid över vattenytan - inget vatten kan komma in oavsett hastighet. I svår sjögång är överbyggnaden under vatten mindre än två sekunder vid varje nerdoppning, men under den korta tiden kommer 180 ton vatten in varje gång - fartyget kör ju med hög fart - 7.45 m/s rätt in under vattnet/vågen och öppningen är 16,2 m². Huss räknar inte med att de nya vikten i överbyggnaden sedan trimmar fartyget. Enbart den första vågen - 180 ton - borde ha stoppat den relativa rörelsen - Estonia hade inte lyft upp fören igen över vattnet, utan plöjt djupare ner under vattnet med ökat trim på fören och fortsatt inflöde. Det borde ha lett till omedelbar kapsejsning. Men låt oss anta att fartyget lyfter fören upp över vattnet efter den första nerdoppningen och det första vattnet lastas akterut i överbyggnaden. Vid nästa nerdoppning efter fem, sex sekunder kommer ytterligare 180 ton in och lastas akterut, osv. Inget vatten rinner ut, pga fart framåt. |
|
Naturligtvis minskar sedan inflödet om farten V minskar. Relativa rörelsens amplitud minskar knappast så länge farten är >10 knop, men antalet nerdoppningar per minut minskar med V, dvs förenklat kan man säga att inflödet minskar med V2. Vid 10 knop är inflödet reducerat 49%, dvs fortfarande ansenligt. Och eftersom besättningen på 'Estonia' aldrig saktade in får man antaga att V>10 knop under minst två minuter, dvs tillräckligt med vatten skulle ha kommit in under den tiden för att kränga färjan upp och ned.
Ökat inflöde pga nerfälld ramp
Ovan tar ej hänsyn till den nerfällda rampen med sina långa flaps i ändan, som i fullt utfällt läge nästan når ner till vattenlinjen (se figur 3.3). Den nerfällda rampen verkar som en plog som redan vid relativ rörelse 0 meter tvingar in vatten upp genom rampöppningen. Det innebär att rampöppningen blir skenbart större och ovan formel för Msp(t) inte är tillämpbar. Det innebär naturligtvis vidare att tiden att fylla bildäck under varje period ökar från 2.2 till 2.8 sekunder (+25%), tiden då rampen är under vatten, men hur mycket extra vatten som kommer in är oklart. Rampen borde ju, om det 55 ton tunga visiret hade dragit ut det helt, först knäckts neråt, över förpiksdäcket, av visiret och sedan knäckts minst 90° eller bakåt runt stäven av kraften i vattnet som 'plogades' in på bildäck. Den maximala rampöppningen under vatten var 3x5.4 dvs 16.2 m². Om rampen, med sina flaps, når ner cirka 2 meter (troligvis mer) under rampöppningen borde man i princip räkna ytterligare 2x5.4 dvs 10.8 m² effektiv inströmningsyta (+67%).
Det innebär att en realistisk inströmning på bildäck under varje nerdoppning inte borde vara 180 m3 under 2.2 sekunder enligt de 'teoretiska' beräkningarna utan troligtvis det dubbla, 360 m3 under 2.8 sekunder. Vattnet skulle då ha fyllt hela rampöppningen nästan upp till däck 4 (öppna väder/backdäck) och krossat allt inne på bildäck. Efter bara fem nerdoppningar - 28 sekunder - skulle 'Estonia' ha slagit runt med 1 800 ton vatten på bildäck. Inflödet med öppen, nerfälld ramp är alltså 3 600 ton/minut. Det är enkelt att verifiera med modellförsök. Fartyget går runt direkt - man hinner knappt starta modellförsöket innan det tar slut. Det var det som hände 'Herald of Free Enterprise' utanför Zeebrügge 1987 - vattnet inte bara strömmade in i överbyggnaden; vattnet trimmade fören under vatten och fartyget kapsejsade direkt! Det är troligtvis därför som slutrapporten inte hänvisar till detta fartyg.
Buller och oväsen när vatten lastas på bildäcket
Att lasta >2 000 ton/min (eller bara 500 ton/min enligt Huss) vatten på ett bildäck i en överbyggnad på en färja till sjöss borde leda till en massa buller och oväsen som borde noteras av alla ombord. Vattnet som trycks in med hög hastighet bör förstöra all lös last i sin väg! Bilar och lastbilar på bildäcket bör tryckas akterut och demoleras hörbart, elektrisk utrustning bör kortslutas, passagerare på däck 1 under bildäcket borde ha hört ett enormt dån under flera minuter när vattnet trycktes in... men hörde ingenting. Huss och Karppinen har aldrig frågat överlevande från däck 1 hur de upplevde att vatten lastades över dem.
Slutsatser
Huss har felberäknat vatteninflödet under den första minuten, när farten var oförändrad och maskinerna gick fullt framåt, med en faktor >7 - Huss säger att vatteninflödet i regelbunden (head waves 15 knop H = 4.0, T = 9.3 sec) är 270 ton/minut, när det i verkligheten är minst 1 940 ton/minut, betydligt mera om rampens inflytande inkluderas.
Karppinen har också felberäknat vatteninflöde i oregelbunden sjö (bow seas, 14.5 knop, Hs=4.3 m) där totala inflödet är cirka 1 560 ton/minut för en typisk sekvens given i Supplement no. 410, medan Karppinen anger en mycket liten sannolikhet för att detta värde uppnås.
Varken Karppinen eller Huss har tagit hänsyn till den nerfällda rampens inflytande på vatteninflödet, dvs att rampen plogar upp vatten in på bildäck. Det borde ha dubblat vatteninflödet och halverat kapsejsningstiden.
Karppinen och Huss tar ej heller hänsyn till att vattnet i överbyggnaden trimmar fartyget. Vattnet som kommer in i överbyggnaden trimmar fartyget på fören, som kommer djupare under vattnet och stoppar den relativa rörelsen uppåt. Resultatet blir att överbyggnaden fylls snabbare än beräknat - kanske på bara halva tiden 12 sekunder - och att sedan färjan slår runt och flyter upp och ned - om inte färjan stannar innan dess ... och allt vatten rinner ut av sig självt!
Karppinens och Huss är så orealistiska i sina beräkningar att man undrar om de är del av en planerad mörkläggning av olyckan (eller om Huss och Karppinen bara är 'användbara, tekniska idioter' utan någon som helst kunskaper om riktiga fartyg och olyckor)? Oavsett - Kommissionens uppgifter om vatteninflöde i överbyggnaden är förfalskade 100%!
Uppdatering 2007
I en rapport av SSPA Marine AB 27 mars 2007 visar modellprov att inflödet genom en öppen bog ramp 2000-2500 tons/min är förväntat.
---